Train Dev Test Data Splits

Made with ❤️ and GitHub Copilot

Data Splitting: Some Thoughts

Data Splitting

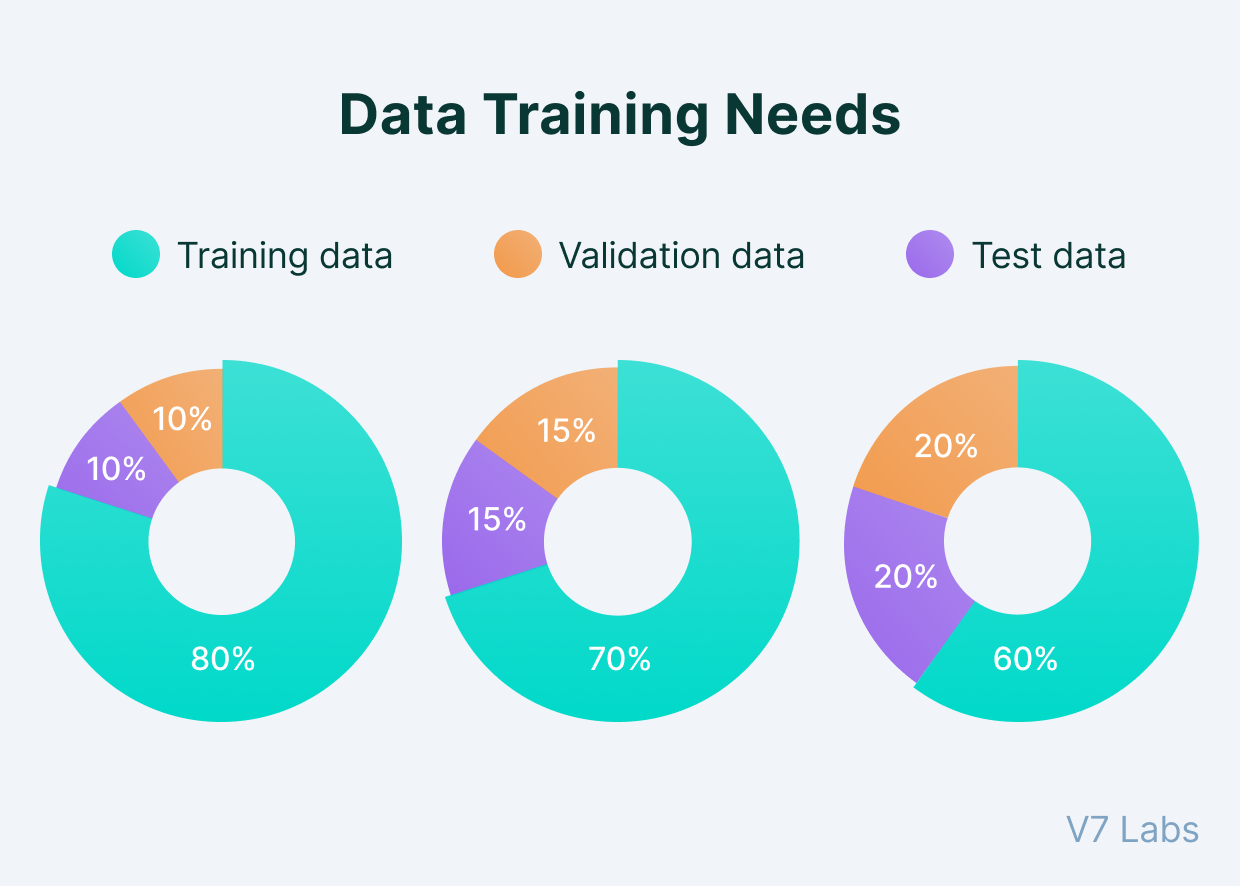
Image from Pragati Baheti at v7labs

Introduction

For good machine learning, selecting the right model and properly splitting your data are crucial steps for success. We explore the process of model selection, drawing parallels between machine learning models and biological speciation, and delves into the details of data splitting and hyperparameter tuning.

Model Selection

To understand model selection better, let’s recap an analogy to biological evolution:

• Models are like different species
• Data represents the environment
• The score function (sometimes called evaluation metric or just metric depending on framework) is akin to survival fitness

The Learning Process

1. Models start in an “newborn state” - they begin with random or preset parameters.
2. They mature and learn by adjusting their parameters based on the training data and available compute resources.
3. The learning process follows a predefined path, often using first-order approximations (like Taylor series) and techniques such as stochastic gradient descent (SGD).
4. The goal is to optimize an appropriate loss function, which guides the model’s adaptation to the data.

Hyperparameters

If models are species, then different hyperparameter configurations can be thought of as subspecies:

• Evaluation depends on the score function, similar to how a species’ success depends on its ability to survive in a specific environment.The score function is chosen to reflect the “survival task”. It could be the same as the loss function, but often is not.
• Well-chosen hyperparameters allow the model to adapt effectively to the given data and task.
• The scoring “environment” is the validation data, and the fitness” is determined by the score function.

Unlike model parameters, hyperparameters cannot be “learned” directly from the data. Instead, they are selected through a process of trial and error, guided by the model’s performance on the validation set. (The trial and error search can be random, but nowadays, more sophisticated methods like Bayesian optimization are often used.)

Note that some frameworks and authors refer to the score function as a metric function of evaluation metric function. The term “metric” is often used in the context of classification tasks, while “loss” is used for regression tasks.

For a mathematician, a metric is a function that measures the distance between two points in a space, but in machine learning, it’s a function that measures the quality of a model’s predictions. Some ML metrics are indeed true metrics, but this is not always the case. This can often lead to puzzling looks from mathematicians when they first encounter machine learning terminology! For example R-squared, MAPE, Huber loss, f1, accuracy, precision, recall, AUC, etc. are all metrics in machine learning, but not in the strict mathematical sense. More on this in a later post.

The Importance of Data Splitting

Before we dive deeper into model selection, it’s essential to understand the concept of data splitting. We typically divide our dataset into three parts:

1. Training set
2. Development (Validation) set
3. Test set

Why Split the Data?

Splitting the data serves several purposes: - The training set is used to teach the model. - The validation set helps us tune the model and select the best hyperparameters. - The test set provides an unbiased evaluation of the final model’s performance.

Factors Affecting Data Splitting

The way we split our data can significantly impact our model’s performance. Let’s explore how this split changes based on various factors:

Amount of Data

The number of examples (n) in the dataset influences the data split. We’ll split by the following (somewhat arbitrary) guidelines:

• Small (n < 1,000): Allocate a larger proportion to the training set.
• Medium (1,000 < n < 100,000): More balanced allocation.
• Large (n > 100,000): Can maintain large training sets while also having substantial validation and test sets.

If the n is 10k or fewer, a widely used practice is combine the train and dev set once a model is selected and retrain on the combined dataset before evaluating on the test set. Sometimes this is called the refit step or refit dataset.

This is less important when the number of examples is large, as additional learning on a usually small validation set is unlikely to improve performance much. Again, this all depends on the nature of the data, it’s number of features, richness, noise and algorithm.

Noise in the Data

• Low noise: Fewer examples needed in validation and test sets.
• High noise: Larger validation and test sets to average out the noise.

Richness of Structure in the Data

• Simple structure: Smaller training sets, larger validation and test sets.
• Complex structure: Larger training sets to learn intricate patterns.

Data Split Table

Here’s a table suggesting possible splits for different dataset sizes, assuming moderate noise and complexity:

Dataset Size (n)	Training Set	Validation Set	Test Set	Example Models/Datasets
100	70-80%	10-15%	10-15%	Small custom datasets, toy problems
1,000	70-75%	15-20%	10-15%	Iris dataset, small NLP tasks
10,000	70-75%	15-20%	10-15%	MNIST, small to medium Kaggle competitions
100,000	70-80%	10-15%	10-15%	CIFAR-100, medium-sized NLP tasks
1 million	80-85%	5-10%	5-10%	ImageNet, large NLP datasets
1 billion	90-95%	2.5-5%	2.5-5%	Very large language models, recommendation systems

Examples of Well-Known Models and Their Data Splits

1. MNIST (70,000 images)
   • Training: 60,000 (85.7%)
   • Test: 10,000 (14.3%)
   • Note: Often, users create their own validation set from the training data.
2. ImageNet (1.2 million images)
   • Training: 1,281,167 (85.4%)
   • Validation: 50,000 (3.3%)
   • Test: 100,000 (6.7%)
3. BERT (BookCorpus + English Wikipedia, ~3.3 billion words)
   • Used a 90-10 split for pre-training and fine-tuning
   • Exact validation and test set sizes vary by downstream task
4. GPT-3 (Trained on 300 billion tokens)
   • Training: Vast majority of the data
   • Test: Varies by task, but typically small (< 1%)
   • Note: Uses few-shot learning, so traditional splits are less applicable
5. Netflix Prize Dataset (~100 million ratings)
   • Training: 98,074,901 (98.1%)
   • Test: 1,408,395 (1.4%)
   • Probe set (public test): 1,408,395 (1.4%)

Implementing Data Splitting in Popular Libraries

Let’s look at how to implement data splitting in three popular machine learning libraries: scikit-learn, Keras, and PyTorch.

# install dependencies
!pip --quiet install datasets tensorflow pandas scikit-learn gdown optuna

We’ll use sentiment140 as our example data, hosted on huggingface by the stanfordnlp group, a dataset of tweets labeled as positive or negative, for our examples. The dataset contains 1.6 million tweets.

The dataset comes pre-split into training and test sets, so we will be a bit contrived and first combine the data splits, before using the combined data to demonstrate the splitting process with some popular libraries.

import os

import pandas as pd
from datasets import concatenate_datasets, load_dataset

# Set the environment variable to disable the prompt
os.environ['HF_DATASETS_OFFLINE'] = '1'

# Load the train and test splits
train_dataset = load_dataset('sentiment140', split='train')
test_dataset = load_dataset('sentiment140', split='test')

# Concatenate the splits
combined_dataset = concatenate_datasets([train_dataset, test_dataset])

# Shuffle the combined dataset
shuffled_dataset = combined_dataset.shuffle(seed=42)

# Convert to a DataFrame
df = shuffled_dataset.to_pandas()

# Separate features (X) and target (y)
X = df.drop(columns=['sentiment'])
y = df['sentiment']

# Print the first 5 examples
print(X.head())
print(X.shape)
print(y.head())
print(y.shape)

                                                text  \
0   External HDD crashed !!! Volumes of data lost
1  @R33S Are you going to her concert in Sydney? ...
2  not as good at super smash bros 64 as I remember
3  I want a convertible. A nice black one - hard ...
4  nooooo! why isn't Public Enemies being release...

                           date      user     query
0  Sun May 31 10:10:40 PDT 2009  twishmay  NO_QUERY
1  Sun May 17 01:20:02 PDT 2009    iB3nji  NO_QUERY
2  Fri Jun 05 23:48:43 PDT 2009    bendur  NO_QUERY
3  Sat May 30 11:46:52 PDT 2009      ihug  NO_QUERY
4  Wed Jun 24 23:16:39 PDT 2009   jssavvy  NO_QUERY
(1600498, 4)
0    0
1    4
2    0
3    4
4    0
Name: sentiment, dtype: int32
(1600498,)

Given this data size, of roughly 1.6 million tweets, we will use the following splits:

Split	Percentage	Number of Examples
Train	80%	1,280,398
Dev	10%	160,050
Test	10%	160,050

This split works with the rule of thumb and is a common practice in the industry. Because of the noise in the data, we want to ensure that we have enough examples in the validation and test sets to get a good estimate of the model’s performance, so we could have increased the size of the validation and test sets. However, for the sake of simplicity, we will stick with this split.

Scikit-learn

from sklearn.model_selection import train_test_split

# Split the data into train and temporary sets (80% train, 20% temp)
X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.2, random_state=42)

# Split the temporary set into validation (dev) and test sets (50% dev, 50% test of the remaining 20%)
X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42)

# Calculate the number of examples
total_examples = len(X)
train_examples = len(X_train)
val_examples = len(X_val)
test_examples = len(X_test)

# Calculate the percentages
train_percentage = (train_examples / total_examples) * 100
val_percentage = (val_examples / total_examples) * 100
test_percentage = (test_examples / total_examples) * 100

# Create a DataFrame to store the split information
split_info = pd.DataFrame({
    'Split': ['Train', 'Dev', 'Test'],
    'Percentage': [f'{train_percentage:.2f}%', f'{val_percentage:.2f}%', f'{test_percentage:.2f}%'],
    'Number of Examples': [train_examples, val_examples, test_examples]
})

# Print the DataFrame
print(split_info)

   Split Percentage  Number of Examples
0  Train     80.00%             1280398
1    Dev     10.00%              160050
2   Test     10.00%              160050

Keras

Let’s do it in Keras now. We’ll use a different dataset - Fashion-MNIST.

This is a dataset of 60,000 28x28 grayscale images of 10 fashion categories, along with a test set of 10,000 images. This dataset can be used as a drop-in replacement for MNIST.

import pandas as pd
from sklearn.model_selection import train_test_split
from tensorflow.keras.datasets import fashion_mnist

# Load the Fashion MNIST dataset
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()

# Split the full training set into train and dev sets (80% train, 20% dev)
X_train, X_dev, y_train, y_dev = train_test_split(X_train_full, y_train_full, test_size=0.2, random_state=42)

# Calculate the number of examples
total_examples = len(X_train_full) + len(X_test)
train_examples = len(X_train)
dev_examples = len(X_dev)
test_examples = len(X_test)

# Calculate the percentages
train_percentage = (train_examples / total_examples) * 100
dev_percentage = (dev_examples / total_examples) * 100
test_percentage = (test_examples / total_examples) * 100

# Create a DataFrame to store the split information
split_info = pd.DataFrame({
    'Split': ['Train', 'Dev', 'Test'],
    'Percentage': [f'{train_percentage:.2f}%', f'{dev_percentage:.2f}%', f'{test_percentage:.2f}%'],
    'Number of Examples': [train_examples, dev_examples, test_examples]
})

# Print the DataFrame
print(split_info)

# Print the shapes of the splits
print(f"Train set shape: {X_train.shape}, {y_train.shape}")
print(f"Dev set shape: {X_dev.shape}, {y_dev.shape}")
print(f"Test set shape: {X_test.shape}, {y_test.shape}")

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
29515/29515 ━━━━━━━━━━━━━━━━━━━━ 0s 2us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26421880/26421880 ━━━━━━━━━━━━━━━━━━━━ 2s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
5148/5148 ━━━━━━━━━━━━━━━━━━━━ 0s 1us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4422102/4422102 ━━━━━━━━━━━━━━━━━━━━ 5s 1us/step
   Split Percentage  Number of Examples
0  Train     68.57%               48000
1    Dev     17.14%               12000
2   Test     14.29%               10000
Train set shape: (48000, 28, 28), (48000,)
Dev set shape: (12000, 28, 28), (12000,)
Test set shape: (10000, 28, 28), (10000,)

PyTorch

from torch.utils.data import DataLoader, random_split
from torchvision import datasets, transforms

# Define the transform (resizing, converting to tensor, normalization)
transform = transforms.Compose([
    transforms.Resize((224, 224)),  # Resize all images to 224x224
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])

# Download and load the Caltech-101 dataset
dataset = datasets.Caltech101(root='data', download=True, transform=transform)

# Split dataset into train (80%), dev (10%), and test (10%)
train_size = int(0.8 * len(dataset))
dev_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - dev_size

train_set, dev_set, test_set = random_split(dataset, [train_size, dev_size, test_size])

# Create DataLoaders for each set
train_loader = DataLoader(train_set, batch_size=32, shuffle=True)
dev_loader = DataLoader(dev_set, batch_size=32, shuffle=False)
test_loader = DataLoader(test_set, batch_size=32, shuffle=False)

for images, labels in train_loader:
    print(images.shape)
    print(labels)
    break 

Files already downloaded and verified
torch.Size([32, 3, 224, 224])
tensor([37, 76, 82,  3,  3, 87,  0, 55,  5,  2,  2,  5, 79, 94, 74, 14, 78,  3,
         3, 86, 54,  5, 68, 28,  3,  0, 21, 61, 85, 31, 56,  0])

Hugging Face

import pandas as pd
from datasets import DatasetDict, load_dataset
from sklearn.model_selection import train_test_split

# Load the emotion dataset
dataset = load_dataset('emotion')

# Convert the dataset to a pandas DataFrame
df = pd.DataFrame(dataset['train'])

# Split the dataset into train and dev sets (80% train, 20% dev)
train_df, dev_df = train_test_split(df, test_size=0.2, random_state=42)

# Convert the DataFrames back to Hugging Face datasets
train_dataset = DatasetDict({'train': dataset['train'].select(train_df.index)})
dev_dataset = DatasetDict({'dev': dataset['train'].select(dev_df.index)})
test_dataset = DatasetDict({'test': dataset['test']})

# Calculate the number of examples
total_examples = len(dataset['train']) + len(dataset['test'])
train_examples = len(train_dataset['train'])
dev_examples = len(dev_dataset['dev'])
test_examples = len(test_dataset['test'])

# Calculate the percentages
train_percentage = (train_examples / total_examples) * 100
dev_percentage = (dev_examples / total_examples) * 100
test_percentage = (test_examples / total_examples) * 100

# Create a DataFrame to store the split information
split_info = pd.DataFrame({
    'Split': ['Train', 'Dev', 'Test'],
    'Percentage': [f'{train_percentage:.2f}%', f'{dev_percentage:.2f}%', f'{test_percentage:.2f}%'],
    'Number of Examples': [train_examples, dev_examples, test_examples]
})

# Print the DataFrame
print(split_info)

# Print the sizes of the splits
print(f"Train set size: {train_examples}")
print(f"Dev set size: {dev_examples}")
print(f"Test set size: {test_examples}")

   Split Percentage  Number of Examples
0  Train     71.11%               12800
1    Dev     17.78%                3200
2   Test     11.11%                2000
Train set size: 12800
Dev set size: 3200
Test set size: 2000

Hyperparameter Tuning and Bayesian Optimization

Choosing the right hyperparameters is crucial for model performance. While grid search and random search are common methods for hyperparameter tuning, Bayesian optimization has emerged as a more efficient alternative, especially for computationally expensive models.

Understanding Bayesian Optimization

Bayesian optimization is a sequential design strategy for global optimization of black-box functions. In the context of machine learning, it’s used to find the best hyperparameters for a given model.

Key concepts in Bayesian optimization include:

1. Surrogate Model: A probabilistic model (often Gaussian Process) that approximates the true objective function (model performance).

2. Acquisition Function: A function that determines which hyperparameter configuration to try next, balancing exploration (trying new areas) and exploitation (focusing on promising areas).

3. Objective Function: The function we’re trying to optimize, typically the model’s performance on a validation set.

How Bayesian Optimization Works

1. Initialize with a few random hyperparameter configurations and evaluate their performance.
2. Fit a surrogate model to these observations.
3. Use the acquisition function to determine the next promising hyperparameter configuration to try.
4. Evaluate the objective function at this new point.
5. Update the surrogate model with the new observation.
6. Repeat steps 3-5 for a specified number of iterations or until a stopping criterion is met.

Advantages of Bayesian Optimization

• More efficient than grid or random search, especially for expensive-to-evaluate objective functions.
• Can handle complex hyperparameter spaces with dependencies between parameters.
• Provides uncertainty estimates for its predictions, allowing for more informed decisions.

Implementing Bayesian Optimization

There are a few well-known libraries for implementing Bayesian optimization in Python, including * hyperopt * keras-tuner * optuna

These libraries provide easy-to-use interfaces for optimizing hyperparameters of machine learning models.

Here’s a simple example using the optuna library to perform Bayesian optimization for a Random Forest Classifier from scikit-learn.

import optuna
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score, train_test_split

# Step 2: Load the dataset
data = load_iris()
X, y = data.data, data.target

# Step 3: Define the objective function
def objective(trial):
    # Define the hyperparameter search space
    n_estimators = trial.suggest_int('n_estimators', 10, 100)
    max_depth = trial.suggest_int('max_depth', 1, 10)
    min_samples_split = trial.suggest_int('min_samples_split', 2, 10)
    min_samples_leaf = trial.suggest_int('min_samples_leaf', 1, 10)
    bootstrap = trial.suggest_categorical('bootstrap', [True, False])
    
    # Create the model with the suggested hyperparameters
    model = RandomForestClassifier(
        n_estimators=n_estimators,
        max_depth=max_depth,
        min_samples_split=min_samples_split,
        min_samples_leaf=min_samples_leaf,
        bootstrap=bootstrap,
        random_state=42
    )
    
    # Perform cross-validation and return the mean score
    score = cross_val_score(model, X, y, cv=3, n_jobs=1, scoring='accuracy').mean()
    return score

# Step 4: Create a study and optimize the objective function
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=50)

# Step 5: Print the results
print(f"Best hyperparameters: {study.best_params}")
print(f"Best cross-validated score: {study.best_value}")

[I 2024-09-19 19:33:06,430] A new study created in memory with name: no-name-32e3b206-2b7e-49ad-81fb-252e23db6c6f
[I 2024-09-19 19:33:06,510] Trial 0 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 71, 'max_depth': 10, 'min_samples_split': 5, 'min_samples_leaf': 3, 'bootstrap': False}. Best is trial 0 with value: 0.9533333333333333.
[I 2024-09-19 19:33:06,550] Trial 1 finished with value: 0.9466666666666667 and parameters: {'n_estimators': 29, 'max_depth': 6, 'min_samples_split': 7, 'min_samples_leaf': 5, 'bootstrap': True}. Best is trial 0 with value: 0.9533333333333333.
[I 2024-09-19 19:33:06,628] Trial 2 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 63, 'max_depth': 5, 'min_samples_split': 5, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 2 with value: 0.9666666666666667.
[I 2024-09-19 19:33:06,675] Trial 3 finished with value: 0.6999999999999998 and parameters: {'n_estimators': 56, 'max_depth': 1, 'min_samples_split': 9, 'min_samples_leaf': 5, 'bootstrap': False}. Best is trial 2 with value: 0.9666666666666667.
[I 2024-09-19 19:33:06,720] Trial 4 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 34, 'max_depth': 8, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:06,802] Trial 5 finished with value: 0.94 and parameters: {'n_estimators': 96, 'max_depth': 7, 'min_samples_split': 4, 'min_samples_leaf': 9, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:06,851] Trial 6 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 38, 'max_depth': 3, 'min_samples_split': 6, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:06,953] Trial 7 finished with value: 0.9333333333333332 and parameters: {'n_estimators': 85, 'max_depth': 1, 'min_samples_split': 10, 'min_samples_leaf': 6, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,026] Trial 8 finished with value: 0.94 and parameters: {'n_estimators': 86, 'max_depth': 9, 'min_samples_split': 3, 'min_samples_leaf': 9, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,081] Trial 9 finished with value: 0.94 and parameters: {'n_estimators': 61, 'max_depth': 6, 'min_samples_split': 6, 'min_samples_leaf': 9, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,143] Trial 10 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 40, 'max_depth': 8, 'min_samples_split': 2, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,208] Trial 11 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 45, 'max_depth': 4, 'min_samples_split': 8, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,236] Trial 12 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 13, 'max_depth': 4, 'min_samples_split': 4, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,268] Trial 13 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 17, 'max_depth': 8, 'min_samples_split': 5, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,356] Trial 14 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 62, 'max_depth': 5, 'min_samples_split': 7, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,403] Trial 15 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 28, 'max_depth': 7, 'min_samples_split': 8, 'min_samples_leaf': 7, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,502] Trial 16 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 72, 'max_depth': 10, 'min_samples_split': 7, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,573] Trial 17 finished with value: 0.96 and parameters: {'n_estimators': 49, 'max_depth': 3, 'min_samples_split': 7, 'min_samples_leaf': 4, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,619] Trial 18 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 28, 'max_depth': 8, 'min_samples_split': 2, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,718] Trial 19 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 70, 'max_depth': 5, 'min_samples_split': 10, 'min_samples_leaf': 7, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,793] Trial 20 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 50, 'max_depth': 9, 'min_samples_split': 8, 'min_samples_leaf': 4, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,884] Trial 21 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 64, 'max_depth': 5, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:07,992] Trial 22 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 80, 'max_depth': 4, 'min_samples_split': 4, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,076] Trial 23 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 58, 'max_depth': 7, 'min_samples_split': 6, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,136] Trial 24 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 38, 'max_depth': 6, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,231] Trial 25 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 67, 'max_depth': 5, 'min_samples_split': 3, 'min_samples_leaf': 4, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,288] Trial 26 finished with value: 0.94 and parameters: {'n_estimators': 53, 'max_depth': 2, 'min_samples_split': 7, 'min_samples_leaf': 2, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,393] Trial 27 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 78, 'max_depth': 3, 'min_samples_split': 6, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,455] Trial 28 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 42, 'max_depth': 5, 'min_samples_split': 3, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,485] Trial 29 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 21, 'max_depth': 10, 'min_samples_split': 3, 'min_samples_leaf': 3, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,538] Trial 30 finished with value: 0.96 and parameters: {'n_estimators': 33, 'max_depth': 7, 'min_samples_split': 4, 'min_samples_leaf': 4, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,608] Trial 31 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 44, 'max_depth': 5, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,677] Trial 32 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 45, 'max_depth': 6, 'min_samples_split': 3, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,730] Trial 33 finished with value: 0.96 and parameters: {'n_estimators': 33, 'max_depth': 4, 'min_samples_split': 5, 'min_samples_leaf': 5, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,772] Trial 34 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 23, 'max_depth': 6, 'min_samples_split': 6, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,839] Trial 35 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 45, 'max_depth': 5, 'min_samples_split': 4, 'min_samples_leaf': 10, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,900] Trial 36 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 57, 'max_depth': 4, 'min_samples_split': 9, 'min_samples_leaf': 3, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:08,955] Trial 37 finished with value: 0.9466666666666667 and parameters: {'n_estimators': 38, 'max_depth': 5, 'min_samples_split': 5, 'min_samples_leaf': 6, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,007] Trial 38 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 32, 'max_depth': 3, 'min_samples_split': 2, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,056] Trial 39 finished with value: 0.9466666666666667 and parameters: {'n_estimators': 42, 'max_depth': 6, 'min_samples_split': 6, 'min_samples_leaf': 5, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,183] Trial 40 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 97, 'max_depth': 7, 'min_samples_split': 7, 'min_samples_leaf': 4, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,254] Trial 41 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 49, 'max_depth': 6, 'min_samples_split': 3, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,324] Trial 42 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 47, 'max_depth': 9, 'min_samples_split': 3, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,401] Trial 43 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 55, 'max_depth': 5, 'min_samples_split': 4, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,465] Trial 44 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 43, 'max_depth': 8, 'min_samples_split': 3, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,541] Trial 45 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 52, 'max_depth': 6, 'min_samples_split': 2, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,627] Trial 46 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 61, 'max_depth': 4, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,673] Trial 47 finished with value: 0.9533333333333333 and parameters: {'n_estimators': 36, 'max_depth': 7, 'min_samples_split': 4, 'min_samples_leaf': 3, 'bootstrap': False}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,719] Trial 48 finished with value: 0.9666666666666667 and parameters: {'n_estimators': 25, 'max_depth': 6, 'min_samples_split': 8, 'min_samples_leaf': 1, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.
[I 2024-09-19 19:33:09,783] Trial 49 finished with value: 0.9733333333333333 and parameters: {'n_estimators': 41, 'max_depth': 4, 'min_samples_split': 3, 'min_samples_leaf': 3, 'bootstrap': True}. Best is trial 4 with value: 0.9733333333333333.

Best hyperparameters: {'n_estimators': 34, 'max_depth': 8, 'min_samples_split': 5, 'min_samples_leaf': 2, 'bootstrap': True}
Best cross-validated score: 0.9733333333333333

When to Use Bayesian Optimization

Bayesian optimization is particularly useful when:

1. The objective function is expensive to evaluate (e.g., training deep neural networks).
2. The hyperparameter space is complex or high-dimensional.
3. You have a limited budget for hyperparameter tuning.

However, for simpler models or when you have ample computational resources, simpler methods like grid search or random search might be sufficient.

Conclusion

Choosing the right data split and tuning hyperparameters are crucial steps in the machine learning pipeline. By considering factors such as dataset size, noise levels, and data complexity, you can optimize your split to balance between model training and performance estimation. Remember, these are guidelines, and the best split for your project may require some experimentation and adjustment.

As you work with larger datasets, you might find that you can allocate smaller percentages to validation and test sets while still maintaining statistical significance. However, always ensure that your validation and test sets are large enough to provide reliable performance estimates for your specific problem.

By understanding the relationships between models, data, and hyperparameters, implementing effective data splitting strategies, and utilizing advanced techniques like Bayesian optimization for hyperparameter tuning, you can make more informed decisions and develop more effective machine learning solutions.